CONTENIDO

Introducción

Capítulo 1 Análisis exploratorio de datos.

1.1. Introducción. 1.2. Variables de respuesta y datos. 1.2.1. Datos cualitativos. 1.2.2. Datos cuantitativos. 1.2.3. Escalas de medición. 1.3. Distribuciones de frecuencia. 1.3.1. Variables cualitativas. 1.3.2. Variables cuantitativas. 1.4. Medidas descriptivas. 1.4.1. Tendencia central. 1.4.2. Percentiles o medidas de posición. 1.4.3. Medidas de dispersión. 1.4.4. Diagrama de caja y brazos. 1.5. Problema de comparación. 1.5.1. Subpoblaciones. 1.5.2. Variable cualitativa. 1.5.3. Variable discreta. 1.5.4. Variable continua. 1.6. Problema de asociación. 1.6.1. Ambas variables ordinales. 1.6.2. Una variable ordinal y otra cuantitativa. 1.6.3. Ambas variables cuantitativas. 1.7. Uso de Excel en análisis exploratorio de datos. 1.7.1. Gráfica de barras. 1.7.2. Histogramas. 1.7.3. Medidas descriptivas. 1.7.4. Diagrama esquemático. 1.7.5. Diagrama de dispersión. 1.7.6. Coeficiente de correlación. 1.8. Ejercicios propuestos. 1.9. Respuestas a los ejercicios propuestos. 1.10. Referencias.

Capítulo 2 Probabilidad.

Introducción. 2.2. Experimentos aleatorios, espacios muestrales y eventos. 2.3. Definiciones de probabilidad. 2.3.1. Definición clásica. 2.3.2. Definición de frecuencia relativa. 2.3.3. Definición subjetiva. 2.4. Repaso de teoría de conjuntos. 2.4.1. Conjuntos y operaciones con conjuntos. 2.5. Relación entre conjuntos y eventos. 2.6. Axiomas de probabilidad. 2.7. Cálculo de probabilidades de eventos. 2.7.1. Probabilidad condicional. 2.7.2. Regla de la multiplicación. 2.7.3. Independencia de eventos. 2.7.4. Teorema de la probabilidad total. 2.7.5. Teorema de Bayes. 2.8. Introducción al cálculo combinatorio. 2.9. Ejercicios propuestos. 2.10. Respuestas a los ejercicios propuestos. 2.11. Referencias.

Capítulo 3 Variables aleatorias y distribuciones de probabilidad.

3.1. Variable aleatoria. 3.1.1. Clasificación de variables aleatorias. 3.2. Función de probabilidad de una variable aleatoria discreta. 3.2.1. Función de distribución acumulada de probabilidad. 3.2.2. Valor esperado o media de una variable aleatoria discreta. 3.2.3. Varianza de una variable aleatoria discreta. 3.3. Función de densidad de probabilidad para variables aleatorias continuas. 3.3.1. Función de distribución acumulada de probabilidades. 3.3.2. Valor esperado o media de una variable aleatoria continua. 3.3.3. Varianza de una variable aleatoria continua. 3.4. Distribuciones de probabilidad bivariadas. 3.4.1. Distribuciones marginales de probabilidad. 3.4.2. Probabilidad condicional de variables aleatorias. 3.4.3. Independencia de variables aleatorias. 3.4.4. Distribución de probabilidad de una función de dos variables aleatorias. 3.4.5. Comportamiento conjunto de dos variables aleatorias. 3.4.6. Correlación entre dos variables aleatorias. 3.4.7. La varianza de una suma de variables aleatorias. 3.4.8. Varianza de una suma de variables aleatorias independientes. 3.5. Ejercicios propuestos. 3.6. Respuestas a los ejercicios propuestos 3.7. Referencias.

Capítulo 4 Algunas distribuciones de probabilidad.

4.1. Introducción. 4.2. Distribución uniforme discreta. 4.2.1. Definición. 4.2.2. Valor esperado y varianza de la distribución uniforme. 4.3. Distribución Bernoulli. 4.3.1. Definición. 4.3.2. Valor esperado y varianza de una distribución Bernoulli. 4.4. Distribución binomial. 4.4.1. Características y definición. 4.4.2. Función de probabilidad binomial. 4.4.3. Esperanza y varianza de una variable aleatoria binomial. 4.4.4. Ejemplos. 4.4.5. Forma geométrica de la distribución binomial. 4.4.6. Selección aleatoria en una población grande. 4.5. Distribución Poisson. 4.5.1. Definición y características. 4.5.2. Valor esperado y varianza de la distribución de Poisson. 4.5.3. Ejemplos. 4.5.4. Función de distribución acumulada. 4.6. Distribución uniforme continua. 4.6.1. Definición y carterísticas. 4.6.2. Valor esperado y varianza de la distribución uniforme continua. 4.6.3. Ejemplo. 4.6.4. Función de distribución acumulada. 4.7. Distribución normal. 4.7.1. Definición. 4.7.2. Valor esperado y varianza de la distribución normal. 4.7.3. Características de la distribución normal. 4.7.4. Regla empírica. 4.7.5. Función de distribución acumulada normal. 4.7.6. Distribución normal estandarizada. 4.7.7. Ejemplos. 4.8. Distribución exponencial. 4.8.1. Definición y características. 4.8.2. Valor esperado y varianza. 4.8.3. Ejemplo. 4.9. Ejercicios propuestos. 4.10. Respuestas a los ejercicios propuestos. 4.11. Referencias.

Capítulo 5 Distribuciones muestrales.

5.1. Introducción. 5.2. Construcción de una distribución de muestreo exacta para 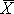. 5.3. Construcción de una distribución de muestreo aproximada para 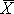. 5.4. Efecto del tamaño de muestra. 5.5. Propiedades de las estadísticas. 5.6. Modelos para distribuciones muestrales. 5.6.1. Distribución de la media muestral. 5.6.2. Distribución de muestreo de la estadística 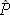. 5.6.3. Distribución de muestreo, de la estadística 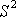. 5.6.4. Distribución de muestreo de 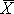cuando es desconocida. 5.6.5. Distribución muestral del cociente de varianzas. 5.7. Referencias.

Capítulo 6 Propiedades de los estimadores y estimación puntual.

6.1. Introducción. 6.2. Estimación puntual. 6.2.1. Definiciones. 6.2.2. Un parámetro, varios estimadores. 6.2.3. Estimadores puntuales más utilizados. 6.3. Propiedades de estimadores. 6.3.1. Motivación. 6.3.2. Esperanza y varianza de un estimador. 6.3.3. Sesgo. 6.3.4. Error Cuadrático Medio (ECM). 6.3.5. Eficiencia relativa. 6.4. Ejercicios de estimación puntual. 6.5. Ejercicios de propiedades de estimadores. 6.6. Ejercicios suplementarios. 6.7. Respuestas a los ejercicios 6.4 y 6.5. 6.8. Referencias.

Capítulo 7 Estimación por intervalos.

7.1. Introducción. 7.1.1. Concepto de intervalo de confianza. 7.1.2. Intervalos aleatorios e intervalos de confianza. 7.1.3. Interpretación de un intervalo de confianza. 7.2. Intervalo de confianza para la media. 7.2.1. Varianza conocida. 7.2.2. Varianza desconocida. 7.3. Intervalo de confianza para la proporción. 7.4. Intervalo de confianza para la varianza. 7.5. Intervalo de confianza para la diferencia de medias (muestras independientes). 7.5.1. Varianzas conocidas. 7.5.2. Varianzas desconocidas. 7.6. Intervalo de confianza para el cociente de varianzas (muestras independientes). 7.7. Intervalo de confianza para la diferencia de medias (muestras dependientes). 7.8. Intervalo de confianza para la diferencia de proporciones (muestras independientes). 7.9. Determinación del tamaño de muestra. 7.9.1. Para la media. 7.9.2. Para la proporción. 7.10. Ejercicios propuestos. 7.11. Respuestas a los ejercicios propuestos. 7.12. Referencias.

Capítulo 8 Pruebas de hipótesis paramétricas.

8.1. Introducción. 8.2. Algunos ejemplos y primeras definiciones. 8.3. Aspectos formales de las pruebas de hipótesis. 8.4. Los riesgos de cometer errores en las pruebas de hipótesis. 8.5. Construcción de criterios para probar hipótesis. 8.6. Algunos comentarios acerca de los errores I y II. 8.7. Pruebas de hipótesis basadas en una muestra aleatoria. 8.7.1. Prueba de hipótesis para una media cuando la varianza es conocida. 8.7.2. Prueba para una media normal con varianza desconocida. 8.7.3. Prueba de hipótesis para una varianza. 8.7.4. Prueba para una proporción. 8.7.5. Prueba para una proporción cuando se tiene un tamaño de muestra grande. 8.8. Nivel de significancia descriptivo o valor p. 8.9. Cálculo de probabilidades de error tipo II. 8.10. Cálculo de tamaño de muestra. 8.11. Pruebas de hipótesis basadas en dos muestras independientes. 8.11.1. Prueba de hipótesis para una diferencia de medias cuando las varianzas son conocidas. 8.11.2. Prueba de hipótesis para una diferencia de medias cuando las varianzas son desconocidas. 8.11.3. Prueba de hipótesis para dos varianzas. 8.12. Pruebas de hipótesis basadas en dos muestras dependientes. 8.12.1. Prueba de hipótesis para una diferencia de medias, por parejas. 8.12.2. Prueba de hipótesis para el coeficiente de correlación ( 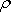). 8.13. Referencias.

Capítulo 9 Pruebas no paramétricas.

9.1. Introducción. 9.1.1. ¿Por qué estadística no paramétrica? 9.1.2. Algo de historia. 9.1.3. No normalidad. 9.2. Pruebas para muestras independientes. 9.2.1. Introducción. 9.2.2. La prueba de igualdad de medianas de Mann-Whitney. 9.2.3. Prueba de Mann-Whitney para muestras grandes. 9.2.4. Prueba de igualdad de varianzas (variante de la prueba de Mann-Whitney). 9.3. Pruebas para muestras pareadas. 9.3.1. La prueba del signo para la mediana de una diferencia. 9.3.2. La prueba de Wilcoxon para la mediana de una diferencia. 9.3.3. La prueba de correlación de Spearman. 9.4. Ejercicios propuestas. 9.5. Respuestas a los ejercicios propuestos. 9.6. Respuestas.

Capítulo 10 Análisis de datos categóricos.

10.1. Introducción. 10.2. Requisitos. 10.3. Notación. 10.4. Algunos conceptos. 10.4.1. Distinción entre atributo y tratamiento. 10.4.2. Datos categóricos. 10.5. Prueba de independencia en tablas de contingencia. 10.5.1. Supuestos. 10.5.2. Tabla de contingencia con las frecuencias esperadas. 10.5.3. Estadística de prueba. 10.5.4. Frecuencias esperadas pequeñas. 10.5.5. Ejemplo. 10.6. Medidas de asociación basadas en la estadística ji-cuadrada. 10.6.1. Coeficiente de contingencia cuadrado medio. 10.6.2. Coeficiente de contingencia en media cuadrática. 10.6.3. Coeficiente de contingencia de Cramêr. 10.7. Ejercicios. 10.8. Glosario. 10.9. Referencias.

Capítulo 11 Muestreo.

Introducción. 11.2. Algunas consideraciones históricas sobre el muestreo. 11.3. Algunos conceptos importantes de estadística. 11.3.1. La estadística y el muestreo. 11.3.2. Algunos conceptos básicos. 11.3.3. Diseño muestral. 11.3.4. Muestreo probabilístico versus muestreo no probabilístico. 11.4. Muestreo Aleatorio Simple(MAS). 11.4.1. Introducción. 11.4.2. Estimación de la media y el total de una variable cuantitativa por MAS. 11.4.3. Tamaños de muestra para la media y el total de una variable cuantitativa por MAS. 11.4.4. Estimación de la proporción y el total para una categoría de una variable cualitativa por MAS. 11.4.5. Tamaños de muestra para la proporción y el total para una categoría de una variable cualitativa por MAS. 11.4.6. ¿Cuándo utilizar MAS? 11.5. Muestreo Aleatorio Estratificado (MAE). 11.5.1. Definición. 11.5.2. Estimación de la media y el total de una variable cuantitativa por MAE. 11.5.3. Tamaños de muestra para la media y el total de una variable cuantitativa por MAE. 11.5.4. Estimación de la proporción y el total para una categoría de una variable cualitativa por MAE. 11.5.5. Tamaños de muestra para la proporción y el total para una categoría de una variable cualitativa por MAE. 11.5.6. ¿Cuándo utilizar MAE? 11.6. Si la aproximación normal no se cumple. 11.7. Errores no muestrales. 11.8. Diseños muestrales más complejos. 11.9. Ejercicios propuestos. 11.10. Respuestas a los ejercicios propuestos. 11.11. Referencias.

Capítulo 12 Números índice.

12.1. Introducción. 12.2. Índices simples: precios, cantidades y valores relativos. 12.3. Índices compuestos o agregados. 12.3.1. Índice de precios de Laspeyres. 12.3.2. Índice de precios de Paasche. 12.3.3. Índice de cantidades de Laspeyres. 12.3.4. Índice de cantidades de Paasche. 12.4. Algunos índices importantes. 12.4.1. Índice Nacional de Precios al Consumidor. 12.4.2. Índice de volumen físico de la actividad industrial. 12.4.3. Deflactor implícito del PIB. 12.4.4. Índice de precios y cotizaciones del mercado bursátil. 12.5. Algunas aplicaciones de los números índice. 12.5.1. Cálculo de la tasa de inflación. 12.5.2. Deflactación de series. 12.5.3. Cálculo del poder adquisitivo de la moneda. 12.6. Consideraciones adicionales sobre los índices. 12.7. Propiedades de los precios, cantidades y datos relativos. 12.8. Ejercicios propuestos. 12.9.Respuestas a los ejercicios propuestos. 12.10. Referencias.

Apéndice.

Números aleatorios. Probabilidades acumuladas de la distribución polinomial. Distribución de Poisson. Distribución normal. Valores críticos de t. Distribución ji-cuadrada. Puntos porcentuales de las distribuciones F. Valores para el Estadístico de Mann-Whitney. Valores para el Estadístico de Wilcoxon (muestras pareadas). Valores para el Estadístico de Correlación de Spearman r_s.